Minimum Swaps to Arrange a Binary Grid

Given an n x n binary grid, in one step you can choose two adjacent rows of the grid and swap them.

A grid is said to be valid if all the cells above the main diagonal are zeros.

Return the minimum number of steps needed to make the grid valid, or -1 if the grid cannot be valid.

The main diagonal of a grid is the diagonal that starts at cell (1, 1) and ends at cell (n, n).

Example 1:

Input: grid = [[0,0,1],[1,1,0],[1,0,0]]
Output: 3

Example 2:

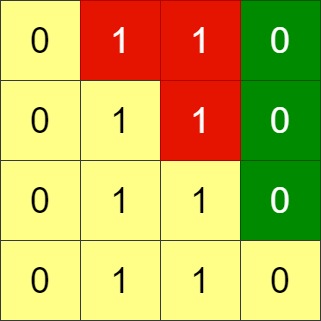
Input: grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]]
Output: -1
Explanation: All rows are similar, swaps have no effect on the grid.

Example 3:

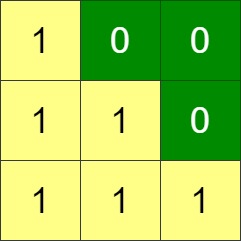
Input: grid = [[1,0,0],[1,1,0],[1,1,1]]
Output: 0

Constraints:

• n == grid.length

• n == grid[i].length

• 1 <= n <= 200

• grid[i][j] is 0 or 1

class Solution {
    public int minSwaps(int[][] grid) {
        int n = grid.length;
        Map<Integer, int[]> map = new HashMap<>();
        Set<Integer> set = new HashSet<>();
        for (int k = n - 1; k > 0; k--) {
            int flag = 0;
            for (int i = 0; i < n; i++) {
                int count = 0;
                for (int j = n - 1; j >= 0; j--)
                    if (grid[i][j] == 0)
                        count++;
                    else
                        break;
                if (count >= k && !set.contains(i)) {
                    flag = 1;
                    set.add(i);
                    map.put(k, new int[]{n - (k + 1), i});
                    break;
                }
            }
            if (flag == 0)
                return -1;
        }
        int count = 0;
        for (int k = n - 1; k > 0; k--) {
            int pos = map.get(k)[1];
            int dest = map.get(k)[0];
            count += Math.abs(pos - dest);
            if (pos > dest) {
                for (int x : map.keySet()) {
                    if (map.get(x)[1] >= dest && map.get(x)[1] < pos)
                        map.get(x)[1]++;
                }
            } else if (pos < dest) {
                for (int x : map.keySet()) {
                    if (map.get(x)[1] > pos && map.get(x)[1] <= dest)
                        map.get(x)[1]--;
                }
            }
        }
        return count;
    }
}