Pseudo-Palindromic Paths in a Binary Tree

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1:

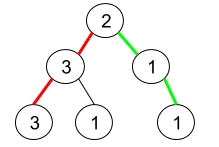
Input: root = [2,3,1,3,1,null,1]
Output: 2 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 2:

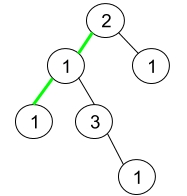
Input: root = [2,1,1,1,3,null,null,null,null,null,1]
Output: 1 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 3:

Input: root = [9]
Output: 1

Constraints:

• The given binary tree will have between 1 and 10^5 nodes.

• Node values are digits from 1 to 9.

class Solution {
    int ans = 0;
    int[] freq;

    public int pseudoPalindromicPaths(TreeNode root) {
        if (root == null)
            return 0;
        freq = new int[10];
        helper(root, 0);
        return ans;
    }

    public void helper(TreeNode root, int oddCount) {
        if (root.left == null && root.right == null) {
            // For a plaindrome permutation ,we must have atmost 1 odd frequency character
            freq[root.val]++;
            if (freq[root.val] % 2 != 0)
                oddCount++;
            else
                oddCount--;
            if (oddCount <= 1)
                ans++;
            freq[root.val]--;
            return;
        }
        freq[root.val]++;
        if (freq[root.val] % 2 != 0)
            oddCount++;
        else
            oddCount--;
        if (root.left != null)
            helper(root.left, oddCount);
        if (root.right != null)
            helper(root.right, oddCount);
        freq[root.val]--;
        return;
    }
}