Sort Items by Groups Respecting Dependencies

There are n items each belonging to zero or one of m groups where group[i] is the group that the i-th item belongs to and it's equal to -1 if the i-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.

Return a sorted list of the items such that:

• The items that belong to the same group are next to each other in the sorted list.

• There are some relations between these items where beforeItems[i] is a list containing all the items that should come before the i-th item in the sorted array (to the left of the i-th item).

Return any solution if there is more than one solution and return an empty list if there is no solution.

Example 1:

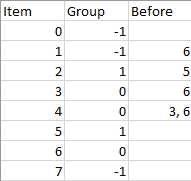
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
Output: [6,3,4,1,5,2,0,7]

Example 2:

Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
Output: []
Explanation: This is the same as example 1 except that 4 needs to be before 6 in the sorted list.

Constraints:

• 1 <= m <= n <= 3*10^4

• group.length == beforeItems.length == n

• -1 <= group[i] <= m-1

• 0 <= beforeItems[i].length <= n-1

• 0 <= beforeItems[i][j] <= n-1

• i != beforeItems[i][j]

• beforeItems[i] does not contain duplicates elements.

class Solution {
    public int[] sortItems(int n, int m, int[] group, List<List<Integer>> beforeItems) {
        // Graph creation with 2 dummy nodes (start & end) for each group
        // We are creating graph like this becuase we want the nodes in 1 group to be
        // together in answer
        List<Integer>[] graph = new ArrayList[n + 2 * m];
        for (int i = 0; i < n + 2 * m; i++)
            graph[i] = new ArrayList<>();
        int[] indegree = new int[n + 2 * m];
        for (int i = 0; i < n; i++) {
            if (group[i] != -1) {
                // Dummy start node to group node
                graph[n + 2 * group[i]].add(i);
                indegree[i]++;
                // group node to dummy end node for that group
                graph[i].add(n + 2 * group[i] + 1);
                indegree[n + 2 * group[i] + 1]++;
            }
            // If 2 different group are involed always make connections with
            // dummy start and end nodes
            for (int x : beforeItems.get(i)) {
                // If "before" is not part of a group
                if (group[x] == -1) {
                    if (group[i] == -1) {
                        graph[x].add(i);
                        indegree[i]++;
                    } else {
                        graph[x].add(n + 2 * group[i]);
                        indegree[n + 2 * group[i]]++;
                    }
                }
                // If "before" is a part of group
                else {
                    if (group[i] == -1) {
                        graph[n + 2 * group[x] + 1].add(i);
                        indegree[i]++;
                    } else {
                        if (group[i] == group[x]) {
                            graph[x].add(i);
                            indegree[i]++;
                        } else {
                            graph[n + 2 * group[x] + 1].add(n + 2 * group[i]);
                            indegree[n + 2 * group[i]]++;
                        }
                    }
                }
            }
        }
        // Topological Sorting
        Deque<Integer> q = new LinkedList<>();
        for (int i = 0; i < n + 2 * m; i++)
            if (indegree[i] == 0)
                q.addLast(i);
        int[] ans = new int[n];
        int index = 0;
        while (q.size() != 0) {
            int node = q.pollFirst();
            for (int x : graph[node]) {
                indegree[x]--;
                // Adding in front of queue, because we want nodes together from same group
                if (indegree[x] == 0)
                    q.addFirst(x);
            }
            if (node < n)
                ans[index++] = node;
        }
        return index == n ? ans : new int[0];
    }
}