Check if There is a Valid Path in a Grid

Given a m x n grid. Each cell of the grid represents a street. The street of grid[i][j] can be:

• 1 which means a street connecting the left cell and the right cell.

• 2 which means a street connecting the upper cell and the lower cell.

• 3 which means a street connecting the left cell and the lower cell.

• 4 which means a street connecting the right cell and the lower cell.

• 5 which means a street connecting the left cell and the upper cell.

• 6 which means a street connecting the right cell and the upper cell.

You will initially start at the street of the upper-left cell (0,0). A valid path in the grid is a path which starts from the upper left cell (0,0) and ends at the bottom-right cell (m - 1, n - 1). The path should only follow the streets.

Notice that you are not allowed to change any street.

Return true if there is a valid path in the grid or false otherwise.

Example 1: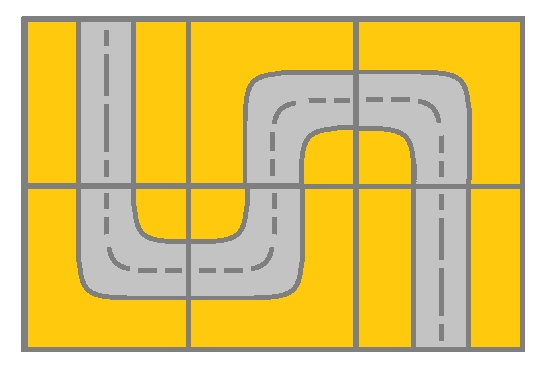

Input: grid = [[2,4,3],[6,5,2]]
Output: true
Explanation: As shown you can start at cell (0, 0) and visit all the cells of the grid to reach (m - 1, n - 1).

Example 2: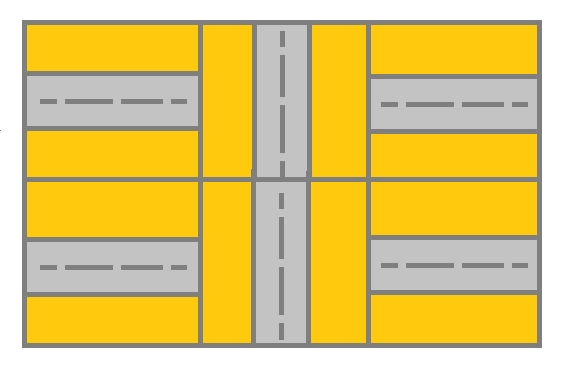

Input: grid = [[1,2,1],[1,2,1]]
Output: false
Explanation: As shown you the street at cell (0, 0) is not connected with any street of any other cell and you will get stuck at cell (0, 0)

Example 3:

Input: grid = [[1,1,2]]
Output: false
Explanation: You will get stuck at cell (0, 1) and you cannot reach cell (0, 2).

Example 4:

Input: grid = [[1,1,1,1,1,1,3]]
Output: true

Example 5:

Input: grid = [[2],[2],[2],[2],[2],[2],[6]]
Output: true

Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 300

• 1 <= grid[i][j] <= 6

public class Solution {
    public boolean hasValidPath(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        return dfs(grid, m, n, 0, 0);
    }

    int[][][] DIR = new int[][][]{
        {{0, -1}, {0, 1}},
        {{-1, 0}, {1, 0}},
        {{0, -1}, {1, 0}},
        {{0, 1}, {1, 0}},
        {{0, -1}, {-1, 0}},
        {{-1, 0}, {0, 1}}
    };

    boolean dfs(int[][] grid, int m, int n, int r, int c) {
        if (r == m - 1 && c == n - 1)
            return true; // Reach bottom-right cell -> Valid path
        int value = grid[r][c];
        grid[r][c] = 0;
        for (int[] nextDir : DIR[value - 1]) {
            int nr = r + nextDir[0], nc = c + nextDir[1];
            if (nr < 0 || nr >= m || nc < 0 || nc >= n || grid[nr][nc] == 0)
                continue;
            for (int[] backDir : DIR[grid[nr][nc] - 1]) {
                // Check if next cell has a connected road
                if (nr + backDir[0] == r && nc + backDir[1] == c) {
                    if (dfs(grid, m, n, nr, nc))
                        return true;
                }
            }
        }
        grid[r][c] = value;
        return false;
    }
}