Critical Connections in a Network

There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some server unable to reach some other server.

Return all critical connections in the network in any order.

Example 1:

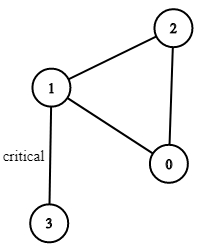
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.

Constraints:

• 1 <= n <= 10^5

• n-1 <= connections.length <= 10^5

• connections[i][0] != connections[i][1]

• There are no repeated connections.

// An edge is a critical connection, if and only if it is not in a cycle.
// We record the timestamp that we visit each node. 
// For each node, we check every neighbor except its parent and return a smallest timestamp in all its neighbors. 
// If this timestamp is strictly less than the node's timestamp, we know that this node is somehow in a cycle. 
// Otherwise, this edge from the parent to this node is a critical connection.

class Solution {
    int T = 1;

    public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
        // use a timestamp, for each node, check the samllest timestamp that can reach
        // from the node
        // construct the graph first
        List<Integer>[] graph = new ArrayList[n];
        for (int i = 0; i < n; i++)
            graph[i] = new ArrayList<>();
        for (List<Integer> conn : connections) {
            graph[conn.get(0)].add(conn.get(1));
            graph[conn.get(1)].add(conn.get(0));
        }
        // an array to save the timestamp that we meet a certain node
        int[] timestamp = new int[n];
        // for each node, we need to run dfs for it, and return the smallest timestamp
        // in all its children except its parent
        List<List<Integer>> criticalConns = new ArrayList<>();
        dfs(graph, timestamp, 0, -1, criticalConns);
        return criticalConns;
    }

    // return the minimum timestamp it ever visited in all the neighbors
    private int dfs(List<Integer>[] graph, int[] timestamp, int currentNode, int parent,
            List<List<Integer>> criticalConns) {
        if (timestamp[currentNode] != 0)
            return timestamp[currentNode];
        timestamp[currentNode] = T++;
        int minTimestamp = Integer.MAX_VALUE;
        for (int neighbor : graph[currentNode]) {
            if (neighbor == parent)
                continue; // no need to check the parent
            int neighborTimestamp = dfs(graph, timestamp, neighbor, currentNode, criticalConns);
            minTimestamp = Math.min(minTimestamp, neighborTimestamp);
        }

        if (minTimestamp >= timestamp[currentNode])
            if (parent >= 0)
                criticalConns.add(Arrays.asList(parent, currentNode));

        return Math.min(timestamp[currentNode], minTimestamp);
    }
}