Number of Closed Islands

Given a 2D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

Example 1:

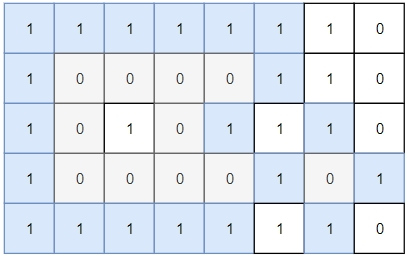
Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation: 
Islands in gray are closed because they are completely surrounded by water (group of 1s).

Example 2:

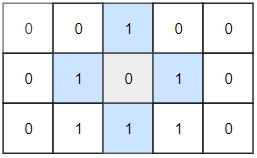
Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1

Example 3:

Input: grid = [[1,1,1,1,1,1,1],
               [1,0,0,0,0,0,1],
               [1,0,1,1,1,0,1],
               [1,0,1,0,1,0,1],
               [1,0,1,1,1,0,1],
               [1,0,0,0,0,0,1],
               [1,1,1,1,1,1,1]]
Output: 2

Constraints:

• 1 <= grid.length, grid[0].length <= 100

• 0 <= grid[i][j] <=1

class Solution {
    public int closedIsland(int[][] grid) {
        // Marking border islands
        boolean[][] visited = new boolean[grid.length][grid[0].length];
        for (int i = 0; i < grid.length; i++) {
            if (grid[i][0] == 0 && !visited[i][0])
                markerDFS(grid, visited, i, 0);
            if (grid[i][grid[0].length - 1] == 0 && !visited[i][grid[0].length - 1])
                markerDFS(grid, visited, i, grid[0].length - 1);
        }
        for (int j = 0; j < grid[0].length; j++) {
            if (grid[0][j] == 0 && !visited[0][j])
                markerDFS(grid, visited, 0, j);
            if (grid[grid.length - 1][j] == 0 && !visited[grid.length - 1][j])
                markerDFS(grid, visited, grid.length - 1, j);
        }
        int count = 0;
        // Counting inner islands
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == 0 && !visited[i][j]) {
                    markerDFS(grid, visited, i, j);
                    count++;
                }
            }
        }
        return count;
    }

    public void markerDFS(int[][] grid, boolean[][] visited, int x, int y) {
        if (x >= 0 && x < grid.length && y >= 0 && y < grid[x].length && grid[x][y] == 0 && !visited[x][y]) {
            visited[x][y] = true;
            markerDFS(grid, visited, x + 1, y);
            markerDFS(grid, visited, x - 1, y);
            markerDFS(grid, visited, x, y + 1);
            markerDFS(grid, visited, x, y - 1);
        }
    }
}