DFS

Depth First Traversal (or Search) for a graph is similar to Depth First Traversal of a tree. The only catch here is, unlike trees, graphs may contain cycles, a node may be visited twice. To avoid processing a node more than once, use a boolean visited array.

Example:

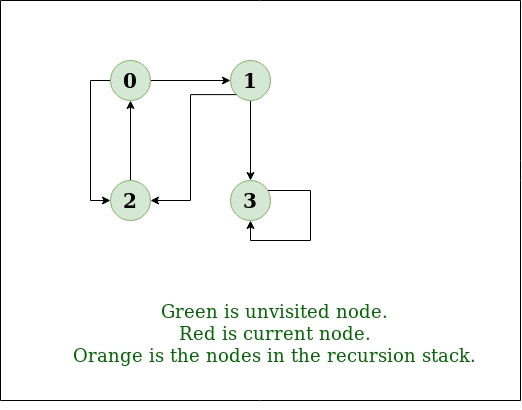
Input: n = 4, e = 6 0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3 Output: DFS from vertex 1 : 1 2 0 3 Explanation: DFS Diagram:

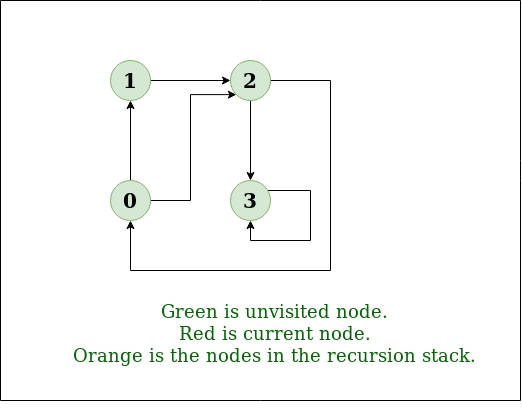
Input: n = 4, e = 6 2 -> 0, 0 -> 2, 1 -> 2, 0 -> 1, 3 -> 3, 1 -> 3 Output: DFS from vertex 2 : 2 0 1 3 Explanation: DFS Diagram:

Recommended: Please solve it on “PRACTICE ” first, before moving on to the solution.

Prerequisites: See this post for all applications of Depth First Traversal.

Following are implementations of simple Depth First Traversal. The C++ implementation uses adjacency list representation of graphs. STL‘s list container is used to store lists of adjacent nodes.

Solution:

• Approach: Depth-first search is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking. So the basic idea is to start from the root or any arbitrary node and mark the node and move to the adjacent unmarked node and continue this loop until there is no unmarked adjacent node. Then backtrack and check for other unmarked nodes and traverse them. Finally print the nodes in the path.

• Algorithm:

  1. Create a recursive function that takes the index of node and a visited array.

  2. Mark the current node as visited and print the node.

  3. Traverse all the adjacent and unmarked nodes and call the recursive function with index of adjacent node.

// Adjacency list
public class solution {

    public static void BFS(ArrayList<Integer> edges[], int sv, boolean visited[]) {
        visited[sv] = true;
        System.out.print(sv + " ");
        for (int x : edges[sv])
            if (!visited[x])
                BFS(edges, x, visited);
    }

    public static void print(ArrayList<Integer> edges[]) {
        boolean[] visited = new boolean[edges.length];
        for (int i = 0; i < edges.length; i++)
            if (!visited[i])
                BFS(edges, i, visited);
    }

    public static void main(String[] args) {
        Scanner s = new Scanner(System.in);
        int V = s.nextInt();
        int E = s.nextInt();
        ArrayList<Integer> edges[] = new ArrayList[V];
        for (int i = 0; i < V; i++)
            edges[i] = new ArrayList<>();
        for (int i = 0; i < E; i++) {
            int fv = s.nextInt();
            int sv = s.nextInt();
            edges[fv].add(sv);
            edges[sv].add(fv);
        }
        print(edges);
        s.close();
    }
}

// Adjacency matrix
public class Solution {

    public static void helper(int edges[][], int sv, boolean visited[]) {
        int n = edges.length;
        visited[sv] = true;
        for (int i = 0; i < n; i++)
            if (edges[front][i] == 1 && !visited[i])
                helper(edges, i, visited);
    }

    public static void print(int edges[][]) {
        boolean[] visited = new boolean[edges.length];
        for (int i = 0; i < edges.length; i++)
            if (!visited[i])
                helper(edges, i, visited);
    }

    public static void main(String[] args) {
        Scanner s = new Scanner(System.in);
        int V = s.nextInt();
        int E = s.nextInt();
        int edges[][] = new int[V][V];
        for (int i = 0; i < E; i++) {
            int fv = s.nextInt();
            int sv = s.nextInt();
            edges[sv][fv] = 1;
            edges[fv][sv] = 1;
        }
        print(edges);
    }
}