LCA in a tree using Binary Lifting Technique

Given a binary tree, the task is to find the Lowest Common Ancestor of the given two nodes in the tree. Let G be a tree then LCA of two nodes u and v is defined as the node w in the tree which is an ancestor of both u and v and is farthest from the root node.If one node is the ancestor of another one than that particular node is the LCA of those two nodes.

Example:

Input:

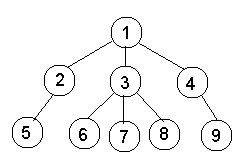
Output: The LCA of 6 and 9 is 1. The LCA of 5 and 9 is 1. The LCA of 6 and 8 is 3. The LCA of 6 and 1 is 1.

class Solution {
    Integer[][] DP;
    int logN;
    Map<Integer, Integer> map;// Map of root -> Depth level

    public void findLCA(TreeNode root, int N, int[][] queries) {
        logN = (int) (Math.ceil(Math.log(N) / Math.log(2))) + 1;
        DP = new Integer[N][logN];
        map = new HashMap<>();
        DFS(root, null, 1);
        for (int[] query : queries)
            System.out.println(LCA(query[0], query[1]));
    }

    public void DFS(TreeNode root, TreeNode parent, int lvl) {
        if (root == null)
            return;
        if (parent != null)
            DP[root.val][0] = parent.val;
        for (int i = 1; DP[root.val][i - 1] != null; i++) {
            int halfDistNode = DP[root.val][i - 1];
            DP[root.val][i] = DP[halfDistNode][i - 1];
        }
        map.put(root.val, lvl);
        DFS(root.left, root, lvl + 1);
        DFS(root.right, root, lvl + 1);
    }

    public int LCA(int P, int Q) {
        // We want P to be lower in tree
        if (lev[P] < lev[Q]) {
            int temp = P;
            P = Q;
            Q = temp;
        }
        // Finding the ansector of P, at the level of Q
        // Starting from the biggest jump and see if it is under range
        for (int i = logN; i >= 0; i--) {
            // Math.pow is slow
            if ((map.get(P) - 1 << i) >= map.get(Q))
                P = DP[P][i];
        }
        if (P == Q)
            return P;
        // Finding the children nodes of LCA
        // Start with the biggest jump, and as soon as we find the biggest jump
        // that results in a node, that is not a common ancestor, we will continue jumps
        // from updates positions.
        for (int i = log; i >= 0; i--) {
            if (DP[P][i] != DP[Q][i]) {
                P = DP[P][i];
                Q = DP[Q][i];
            }
        }
        // Returning the first ancestor of above found nodes
        // As this will be the common ancestor
        return DP[P][0];
    }
}