Eulerian path and circuit for undirected graph

Assume connected graph

Eulerian Path is a path in graph that visits every edge exactly once. Eulerian Circuit is an Eulerian Path which starts and ends on the same vertex.

How to find whether a given graph is Eulerian or not? The problem is same as following question. “Is it possible to draw a given graph without lifting pencil from the paper and without tracing any of the edges more than once”.

A graph is called Eulerian if it has an Eulerian Cycle and called Semi-Eulerian if it has an Eulerian Path. The problem seems similar to Hamiltonian Path which is NP complete problem for a general graph. Fortunately, we can find whether a given graph has a Eulerian Path or not in polynomial time. In fact, we can find it in O(V+E) time.

Following are some interesting properties of undirected graphs with an Eulerian path and cycle. We can use these properties to find whether a graph is Eulerian or not.

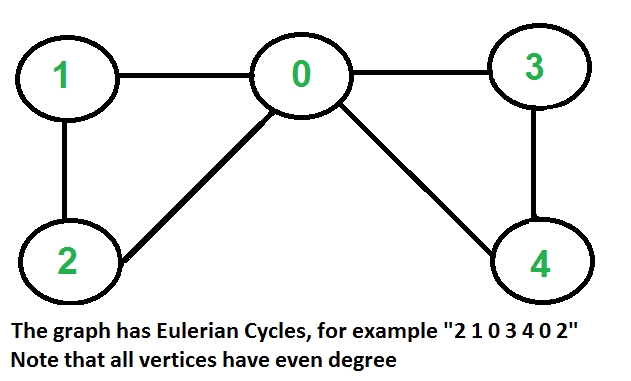
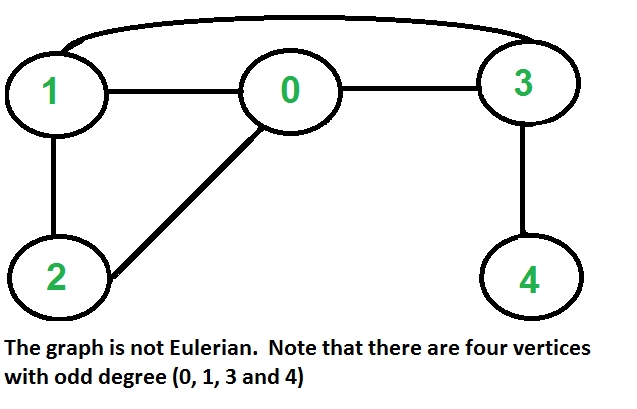
Eulerian Cycle An undirected graph has Eulerian cycle if following two conditions are true. ….a) All vertices with non-zero degree are connected. We don’t care about vertices with zero degree because they don’t belong to Eulerian Cycle or Path (we only consider all edges). ….b) All vertices have even degree.

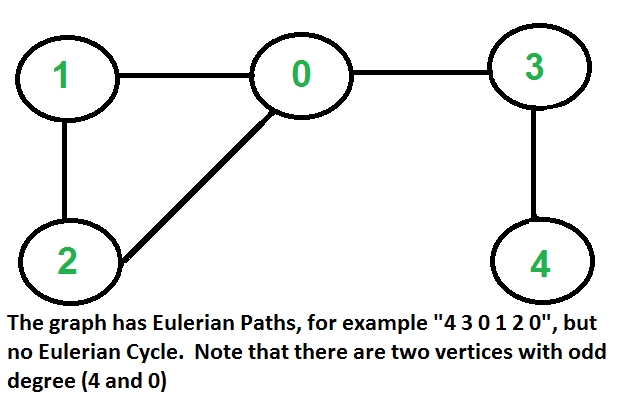
Eulerian Path An undirected graph has Eulerian Path if following two conditions are true. ….a) Same as condition (a) for Eulerian Cycle ….b) If zero or two vertices have odd degree and all other vertices have even degree. Note that only one vertex with odd degree is not possible in an undirected graph (sum of all degrees is always even in an undirected graph)

Note that a graph with no edges is considered Eulerian because there are no edges to traverse.

How does this work? In Eulerian path, each time we visit a vertex v, we walk through two unvisited edges with one end point as v. Therefore, all middle vertices in Eulerian Path must have even degree. For Eulerian Cycle, any vertex can be middle vertex, therefore all vertices must have even degree.

class Solution {
    public static boolean isCircuit(int[][] graph) {
        int oddCount = 0;
        for (int i = 0; i < graph.length; i++) {
            int edges = 0;
            for (int j = 0; j < graph.length; j++)
                edges += graph[i][j];
            if (edges % 2 != 0)
                oddCount++;
        }
        return oddCount == 0;
    }

    public static boolean isPath(int[][] graph) {
        int oddCount = 0;
        for (int i = 0; i < graph.length; i++) {
            int edges = 0;
            for (int j = 0; j < graph.length; j++)
                edges += graph[i][j];
            if (edges % 2 != 0)
                oddCount++;
        }
        if (oddCount == 2 || oddCount == 0)
            return true;
        return false;
    }

    public static void main(String[] args) {
        // code
        Scanner s = new Scanner(System.in);
        int t = s.nextInt();
        while (t-- > 0) {
            int n = s.nextInt();
            int graph[][] = new int[n][n];
            for (int i = 0; i < n; i++)
                for (int j = 0; j < n; j++)
                    graph[i][j] = s.nextInt();
            if (isPath(graph))
                System.out.println("1");
            else
                System.out.println("0");
        }
        s.close();
    }
}