Total number of different staircase that can made from N boxes

Given N boxes each of unit dimension i.e. (1×1 ). The task is to find the total number of different staircases that can be made from those boxes with the following rules:

• Staircase must be in strictly descending order.

• Each staircase contains at least two steps. (Total steps is equal to the breadth of the staircase.)

Examples:

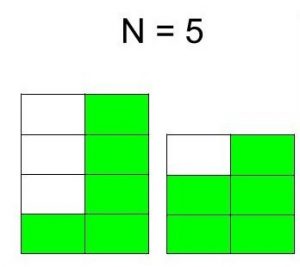
Input : N = 5 Output : 2 The two staircase are following :

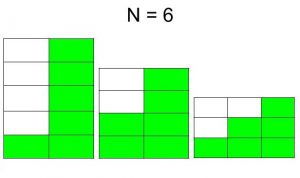
Input : N = 6 Output : 3 The three staircase are following :

If we consider total steps = 2, we can observe the fact that the number of staircase is incremented by 1 if N is incremented by 2. We can illustrate the above thing from the following image :

Now, if total steps is greater than 2 (assume, total steps = K) then we can take this thing as first create a base (base requires boxes equal to the total steps) for staircase and put another staircase on it of steps size K and K – 1 having boxes N – K. (because K boxes already used to create base). Thus, we can solve this problem using bottom-up dynamic programming.

public class Solution {
    public int countStaircases(int N) {
        // dp[i][j] -> number of stair cases possible with i bricks which has j
        // width(steps)
        int[][] dp = new int[N][N];
        // Base case
        dp[3][2] = dp[4][2] = 1;
        for (int i = 5; i <= N; i++) {
            for (int j = 2; j <= i; j++) {
                // When step is equal to 2
                if (j == 2)
                    dp[i][j] = dp[i - j][j] + 1;
                // When step is greater than 2
                else
                    dp[i][j] = dp[i - j][j] + dp[i - j][j - 1];
            }
        }

        int answer = 0;
        for (int i = 1; i <= N; i++)
            answer = answer + dp[N][i];

        return answer;
    }
}